In part 2 of this tutorial series we created the game level and we prepared the player characters.
In this part we will create the player’s movement and jump functionality, and we will animate the player through code.
The Player Script
Now we have everything ready to start coding the player’s movement. In the Project tab under Assets Right Click -> Create -> Folder name it Scripts. In the Scripts folder create a new folder and name it Player Scripts.
Inside the Player Scripts folder Right Click -> Create -> C# Script, name it Player and attach it on the Player 1 game object:
The first thing that we are going to do is move the player character. For that open the Player script and add the following variables above the Start function declaration:
[SerializeField]
private float moveSpeed = 10f;
private float movementX;
The moveSpeed variable is going to control how fast we are moving, I added SerializeField above it so that we can change that value directly in the Inspector tab if there is a need for that.
The movementX will get the movement input from the user when he presses a button on his keyboard to move the player left or right.
To do this, we are going to create a function that will handle the player’s movement:
void HandlePlayerMovement()
{
movementX = Input.GetAxisRaw("Horizontal");
transform.position += new Vector3(movementX, 0f, 0f) * moveSpeed * Time.deltaTime;
}
Input.GetAxisRaw will return -1 if we press A or Left Arrow key on the keyboard. It will return 1 if we press D or Right Arrow key on the keyboard and it will return 0 if we don’t press any of those keys. We will store the returned value in the movementX variable.
After that, we take the current position and add to it a new Vector3 where we pass the movementX variable as the parameter for the X axis, for the Y and Z we provide 0 because we are not moving on those axis and we simply multiply that with the moveSpeed and deltaTime.
Time.deltaTime is used to smooth out the movement when we are moving a game object using its transform property.
To test this, call the HandlePlayerMovement function in the Update:
void Update()
{
HandlePlayerMovement();
}
Run the game and test it:
Setting Up Best Coding Practices
In the HandlePlayerMovement function we are passing a string in the GetAxisRaw function to get the horizontal movement of the player.
One thing that I don’t like when it comes to passing parameters that will never change is hard coding them.
The issue that can arise with this approach is that we can make typo somewhere in the code and it will cause issues for the project.
Of course, when a project is small this is very easy to fix, but when your projects expands to a larger scale then it will become difficult to deal with these things.
So what I like to do is create a static class called TagManager and I put all the parameter values that I will use as static variables inside that class.
If you don’t know what is a static class you can learn about that topic here.
Inside the Assets -> Scripts folder, Right Click -> Create -> Folder and name it Helper Scripts.
Inside the Helper Scripts folder Right Click -> Create -> C# Script and name it TagManager.
Inside the TagManager script you can remove all declarations that come with default and simply declare it as a static class:
public static class TagManager
{
}
Now we can declare a new static string variable that we will use as a parameter for the GetAxisRaw function:
public static class TagManager
{
public static string HORIZONTAL_AXIS = "Horizontal";
}
Change the code inside the HandlePlayerMovement function to use the HORIZONTAL_AXIS variable from the TagManager script instead of the hard coded string value:
void HandlePlayerMovement()
{
movementX = Input.GetAxisRaw(TagManager.HORIZONTAL_AXIS);
transform.position += new Vector3(movementX, 0f, 0f) * moveSpeed * Time.deltaTime;
}
This way we have the same result but our code is set up better. If there is any problem and something is not working, we just need to go inside the TagManager script and fix the issue.
Facing The Moving Direction
Now while the player character is moving he is not facing the movement direction.
There are two ways how we can fix this issue, one using the scale property of the transform component and the other using the sprite renderer component.
In my Rainy Knifes tutorial I’ve used the sprite renderer component to change the facing direction of the player character, so in this tutorial I am going to demonstrate how to do the same thing using the scale property.
First we are going to declare a new Vector3 variable inside the Player script:
private Vector3 tempScale;
Next, we are going to create a new function that will handle the facing direction of the player:
void HandleFacingDirection()
{
tempScale = transform.localScale;
if (movementX > 0)
tempScale.x = Mathf.Abs(tempScale.x);
else if (movementX < 0)
tempScale.x = -Mathf.Abs(tempScale.x);
transform.localScale = tempScale;
}
Inside the HandleFacingDirection function we first get the current value of the scale by calling transform.localScale.
To understand how to change the facing direction, we need to understand Unity’s coordinate system. Since we are moving the player left and right, we need to know that the left side is the negative side and the right side is the positive side in Unity.
With that information we can use the movementX variable to our advantage, because when we press the A or the Left Arrow key the Input.GetAxisRaw will return -1, which means we are going to the left side because it’s a negative number.
And when we press the D or the Right Arrow key the Input.GetAxisRaw will return 1, which means we are going to the right side because it’s a positive number.
That is why we are testing if movementX is greater than 0 we will set the localScale.x to the absolute value of localScale.x.
Now what does that mean?
First of all, Mathf.Abs will return an absolute number. An absolute number is always positive, so if we pass 2 or -2 as the value in the Mathf.Abs function, it will return 2, because absolute values are always positive as I said.
So why am I using this function to set the value of the scale when I can simply use -1 and 1?
The reason why is sometimes in your games you will change the scale of your game object, in our case we didn’t change the scale and we are using the default scale which is 1, and you can verify that by selecting Player 1 game object in the Hierarchy tab and check the Scale values in the Transform component:
In this case we can use 1 and -1 to change the scale of the game object and it will work.
But what if we changed the scale of Player 1 to 0.5 for example, not a problem, we would have to use 0.5 and -0.5 in our code to flip the game object.
So instead of the need to memorize which scale value we are using for the game object, we can simply use scale value and pass it in the Mathf.Abs function and it will return that same value but as a positive number.
So essentially Mathf.Abs is a shortcut so that we don’t have to hard code values for the scale with real numbers.
Now since the Mathf.Abs value always returns a positive number, we need to use the minus or the negative sign – on line 8 in front of the Mathf.Abs function because the returned value will be positive but the minus sign will make it negative.
After that we simply reassign the scale value back to the transform.localScale property and that is how we are flipping Player 1 game object depending on the direction he is moving.
Make sure that you call the HandleFacingDirection in the Update function:
void Update()
{
HandlePlayerMovement();
HandleFacingDirection();
}
Now let’s play the game to test it out:
Animating The Player Through Code
Now that the player character is moving and facing the direction of his movement we need to animate the player.
In the Player script declare a new Animator variable:
private Animator anim;
In the Awake function we are going to get a reference to the Animator component:
private void Awake()
{
anim = GetComponent<Animator>();
}
I always use Awake function to get a reference to components and game objects that we need in the script.
There are other initialization functions that can be used for this purpose as well, you can read more about them here.
Before we proceed to create a function that will handle the player’s animations, inside the TagManager script add the following line:
public static string WALK_ANIMATION_PARAMETER = "Walk";
Since we are calling the parameters we created in the Animator tab using their name as a string, we might as well create a variable for that in the TagManager so that we don’t hard code that value:
void HandlePlayerAnimation()
{
if (movementX != 0)
anim.SetBool(TagManager.WALK_ANIMATION_PARAMETER, true);
else
anim.SetBool(TagManager.WALK_ANIMATION_PARAMETER, false);
}
Again we can use the value of movementX variable to our advantage. This time we are testing if movementX is not equal to 0 meaning that the player character is moving to the left or to the right.
We don’t care if the player character is moving to the negative or the positive side when it comes to animating him, we only care that is moving.
So if the player character is moving we call the SetBool function on the Animator and pass true, because if you remember in the Animator tab the transition condition from Idle to Walk animation is when the value for the Walk parameter is true:
And when the movementX variable returns 0 that means that our player character is not moving so this time we pass false as the second parameter in the SetBool function which is the transition condition from Walk to Idle animation:
Call the HandlePlayerAnimation inside the Update function:
void Update()
{
HandlePlayerMovement();
HandleFacingDirection();
HandlePlayerAnimation();
}
Let’s run the game and test the animation out:
We see that the player’s animation is working but it looks weird as the player is flapping his hands like a crazy person.
How can we fix this?
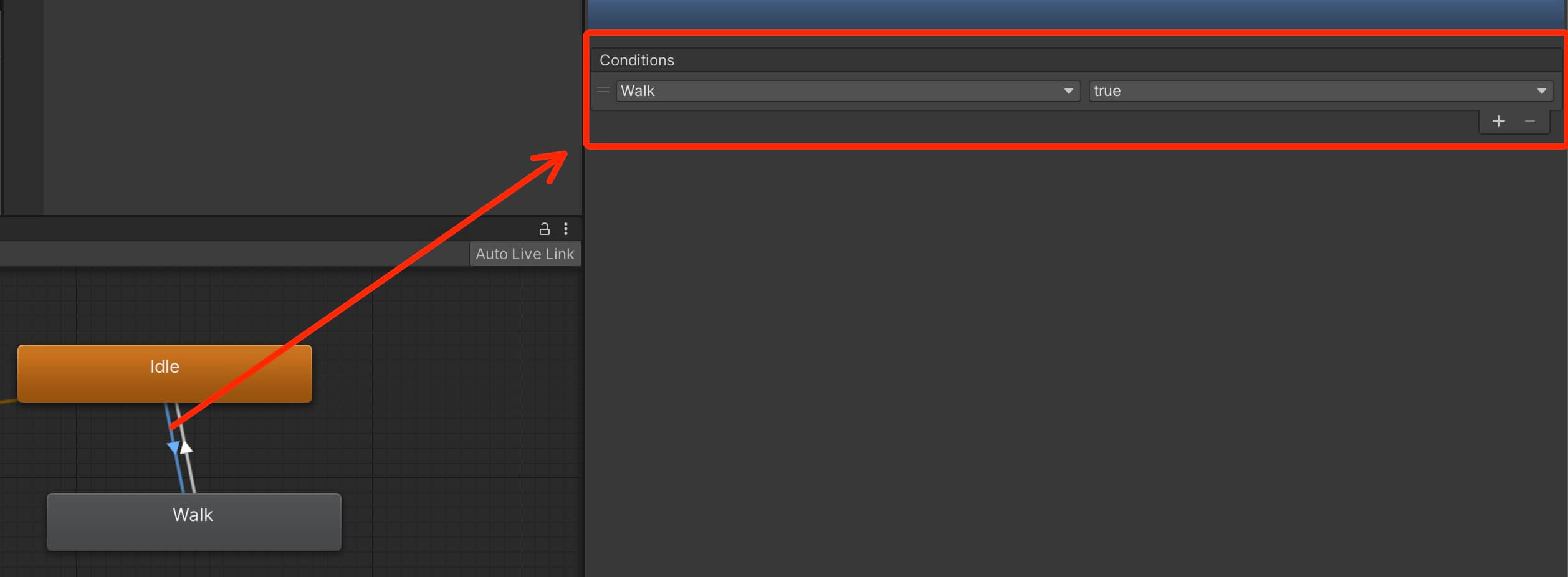
Changing The Speed Of Animations
The issue that we have with the animations is the matter of the speed by which the animation is played.
One of the ways how we can fix this is by playing with the sample rate values. You can follow this guide by clicking here to help you change the speed of the Walk animation.
If you are still not satisfied with the outcome, you can also change the speed of the animation from the Animator tab. You can follow this guide by clicking here to help you change the speed of the animation in the Animator tab.
I’ve set the sample rate to 24 and set the speed of the animation in the Animator tab to 0.7.
Of course you are not obligated to set the same values for the animation speed, but I am sharing with you the values that I’ve set. You can play with the values until you are satisfied with the outcome.
This is how the animation looks like now:
The player character is not flapping with his hands like a crazy person and the animation looks good now, but another issue that we have is that the transitions between animations are late.
Because of that you see how the player is sliding on the ground instead of playing the walk animation.
What is the issue here?
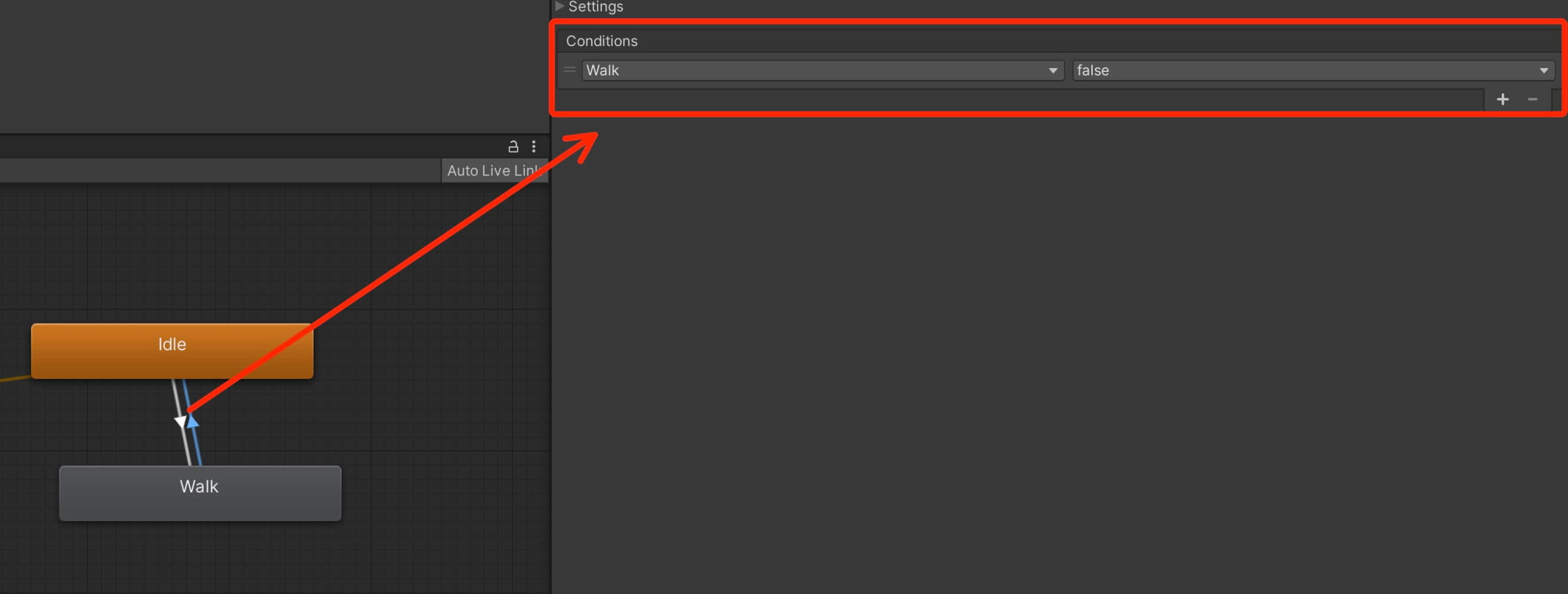
Fixing The Speed Of The Animation Transition
The transitions we set up for the animations also have settings that will make those transitions play quicker or slower e.g. the transition from one animation to another will happen faster or slower.
They also have settings that will make the transition wait for the current animation to finish playing before it transitions to the next animation.
That is the reason why sometimes we see the player character sliding on the ground instead of playing the Walk animation, because the transition from Idle to Walk animation waits for the Idle animation to finish playing before it transitions to the Walk animation.
To fix this, in the Animator tab select the transition from Idle to Walk and locate the Settings drop down list in the Inspector tab:
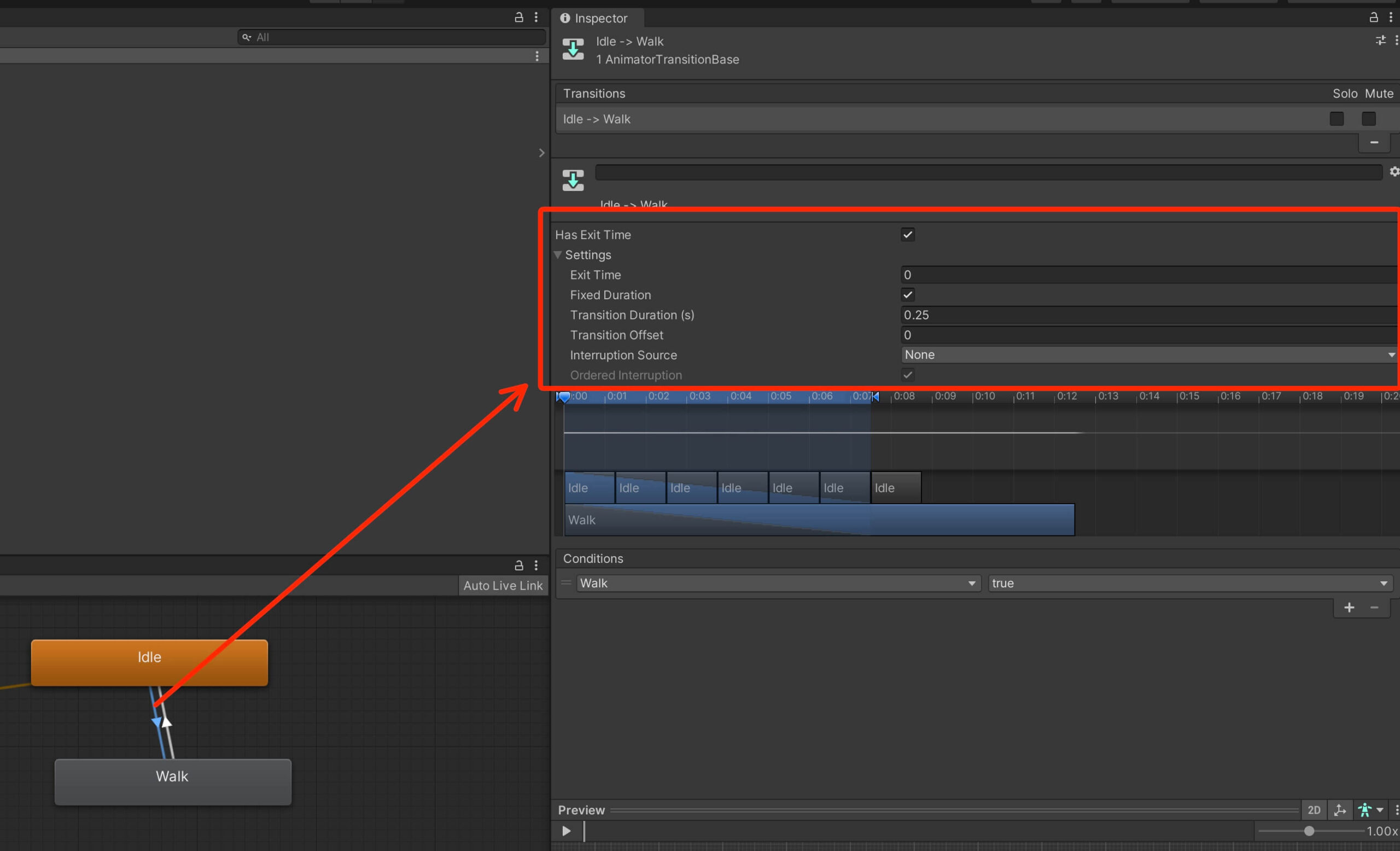
Change the values in the Settings for the transition to following:
Do the same thing for the transition from Walk to Idle animation and set the same values in the Settings for that transition.
Let’s test the animation now:
Now when we move the Walk animation plays without any delays and the same thing goes when we stop moving, the Walk animation stops and the Idle animations starts playing without any delays.
Player Jump Functionality
The next step is to make the player character jump so that he can avoid the wave of enemies that comes towards him.
As always, we need a few variables for that. Inside the Player script add the following variables:
private Rigidbody2D myBody;
[SerializeField]
private float jumpForce = 8f;
private bool isGrounded;
We are going to use the Rigidbody2D component from the player character and apply force to it to make the player jump.
The jumpForce is the value that we are going to use to determine how far can the player jump. I’ve added the SerializeField keyword above it so that it is visible in the Inspector panel and we can always edit the value if there is a need for it.
And lastly, the isGrounded variable will tell us if the player character is on the ground, if he is, then we can jump, if he is not, then we can’t jump.
The first thing we need to do is get a reference to the Rigidbody2D. Inside the Awake function below the line of code where get the Animator reference add the code that will get the Rigibody2D reference:
private void Awake()
{
anim = GetComponent<Animator>();
myBody = GetComponent<Rigidbody2D>();
}
Before we create the jump function, inside the TagManager class, add the following variable:
public static string JUMP_BUTTON_ID = "Jump";
Now we can create the jump function:
void HandleJumping()
{
if (Input.GetButtonDown(TagManager.JUMP_BUTTON_ID) && isGrounded)
{
isGrounded = false;
myBody.AddForce(new Vector2(0f, jumpForce), ForceMode2D.Impulse);
}
}
We calling the GetButtonDown function from the Input class and we are passing it the variable that we created a moment ago in the TagManager class.
Passing the string Jump value as the parameter in the GetButtonDown will call the button that is usually used as a jump button for the appropriate platform. For PC that would be Space, for Consoles that would be X, and so on.
In the testing condition, we are testing if we press down the button, this is really important to know, because the GetButtonDown function will return true only when we press the appropriate button down on our keyboard.
Along with that test we are also testing if the isGrounded variable is true, meaning if we press the jump button and the player is on the ground only then we will jump.
When the condition evaluates to be true the first thing that we are doing is setting the isGrounded to false to prevent the player from double jumping.
Next we add force to the Rigidbody2D by calling the AddForce function and providing a new Vector2 with 0 for the X and jumpForce for the Y parameter. This will make the player jump on the Y axis and no force will be applied on the X axis.
The ForceMode2D.Impulse will add an instant force to the Rigidbody2D using it’s mass. If we don’t use ForceMode2D.Impulse as the second parameter then the force applied to the Rigidbody2D will not be instant, and you can easily test this out by simply removing the ForceMode2D.Impulse parameter after we perform the initial test so that you can see the difference.
Before we proceed, make sure that you call the HandleJumping function inside the Update:
void Update()
{
HandlePlayerMovement();
HandleFacingDirection();
HandlePlayerAnimation();
HandleJumping();
}
Now we are still not done because there is one more step to take.
We need to have a way to know that the player character is on the ground, because if the isGrounded variable is false, then we will not be able to jump.
First, we need to add the following line of code in the TagManager class:
public static string GROUND_TAG = "Ground";
Next, create a new Ground tag and tag the Game Ground game object with the Ground tag:
If you don’t know how to create a new tag and tag a game object, you can learn that here.
Now we can test for collision inside the Player class using the OnCollisionEnter2D function:
private void OnCollisionEnter2D(Collision2D collision)
{
if (collision.gameObject.CompareTag(TagManager.GROUND_TAG))
isGrounded = true;
}
The OnCollisionEnter2D function will give us information about the game object we have collided in the form of the Collision2D parameter.
That’s why, we can use that parameter and call its gameObject property and perform the tag test using the CompareTag function which will tell us if the game object we have collided with has the tag that we provided as the parameter in the CompareTag function in our case the Ground tag.
Keep in mind that the tag name in the code and the tag name in the editor need to match with capitalization or otherwise the test will not work.
So if we declared a tag Ground in the editor, in the code we need to test with another Ground, if we use ground with lower case g, it will not work.
If the comparison above is true, then the isGrounded variable will be set to true and we will be able to jump.
Let’s run the game to test it out:
As you can see, every time the player character lands on the ground he is able to jump. If you try to jump while you are in the sky already, then you will not be able to until the player lands on the ground again.
One thing that we did notice is that the player is jumping weirdly, like is he floating in the air.
How can we fix this?
Editing The Settings For Rigidbody2D
We are using the Rigidbody2D component to make the player jump. The Rigidbody2D component applies gravity to the game object and it allows forces to affect the game object.
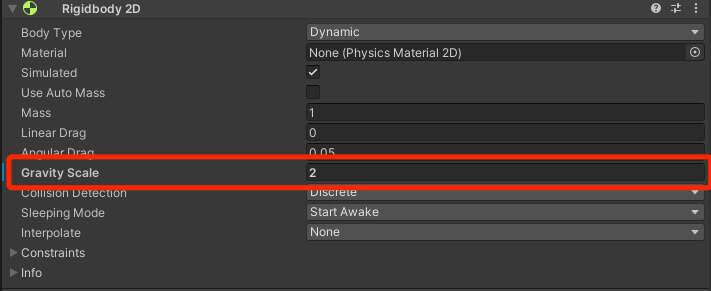
For the current situation where the player character is jumping weirdly, we can double the gravity effect on the player game object by changing the value of the Gravity Scale from 1 to 2 inside the Rididbody2D component:
While we are at it, we can also freeze the Z rotation in the Constraints option for the Rigidbody2D:
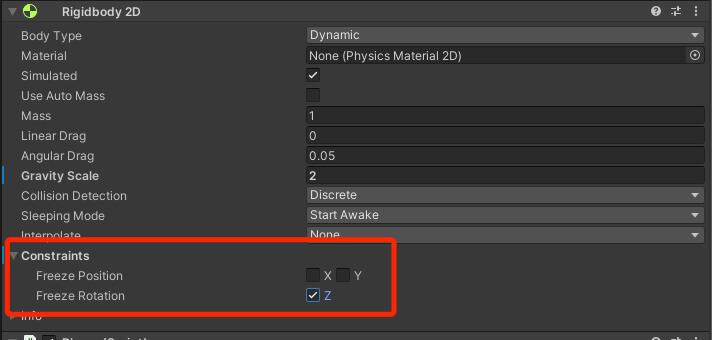
Freezing the Z rotation in the Constraints option will prevent the player game object from rolling over. For more information about this issue, you can click here.
Let’s test the game now and see the outcome:
Player’s jump has greatly improved by setting the Gravity Scale value to 2, however the player character didn’t jump far enough in the sky.
To be able to jump over enemies I’ve set the value of jumpForce for the Player script in the Inspector to 11 as you saw in the video:
Make sure that you override the changes we made to the player by pressing Apply All button so that the changes will be applied to the original prefab:
And with that we finished the Player script. As a reference, I am going to leave the finished Player script down below if you need to copy some lines of code in your project:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Player : MonoBehaviour
{
[SerializeField]
private float moveSpeed = 10f;
private float movementX;
private Vector3 tempScale;
private Animator anim;
private Rigidbody2D myBody;
[SerializeField]
private float jumpForce = 8f;
private bool isGrounded;
private void Awake()
{
anim = GetComponent<Animator>();
myBody = GetComponent<Rigidbody2D>();
}
// Update is called once per frame
void Update()
{
HandlePlayerMovement();
HandleFacingDirection();
HandlePlayerAnimation();
HandleJumping();
}
void HandlePlayerMovement()
{
movementX = Input.GetAxisRaw(TagManager.HORIZONTAL_AXIS);
transform.position += new Vector3(movementX, 0f, 0f) * moveSpeed * Time.deltaTime;
}
void HandleFacingDirection()
{
tempScale = transform.localScale;
if (movementX > 0)
tempScale.x = Mathf.Abs(tempScale.x);
else if (movementX < 0)
tempScale.x = -Mathf.Abs(tempScale.x);
transform.localScale = tempScale;
}
void HandlePlayerAnimation()
{
if (movementX != 0)
anim.SetBool(TagManager.WALK_ANIMATION_PARAMETER, true);
else
anim.SetBool(TagManager.WALK_ANIMATION_PARAMETER, false);
}
void HandleJumping()
{
if (Input.GetButtonDown(TagManager.JUMP_BUTTON_ID) && isGrounded)
{
isGrounded = false;
myBody.AddForce(new Vector2(0f, jumpForce), ForceMode2D.Impulse);
}
}
private void OnCollisionEnter2D(Collision2D collision)
{
if (collision.gameObject.CompareTag(TagManager.GROUND_TAG))
isGrounded = true;
}
} // class
CameraFollow Script
Before we wrap this lecture up, we are going to create the script that will make the camera follow the player character.
Inside the Assets -> Scripts folder, Right Click -> Create -> Folder and name it Camera Scripts.
Inside the Camera Scripts folder Right Click -> Create -> C# Script and name it CameraFollow.
Make sure that you attach the CameraFollow script on the Main Camera game object in the Hierarchy:
Next, inside the CameraFollow script, we are going to add variables that we need to make the camera follow the player character:
private Transform playerTarget;
private Vector3 tempPos;
[SerializeField]
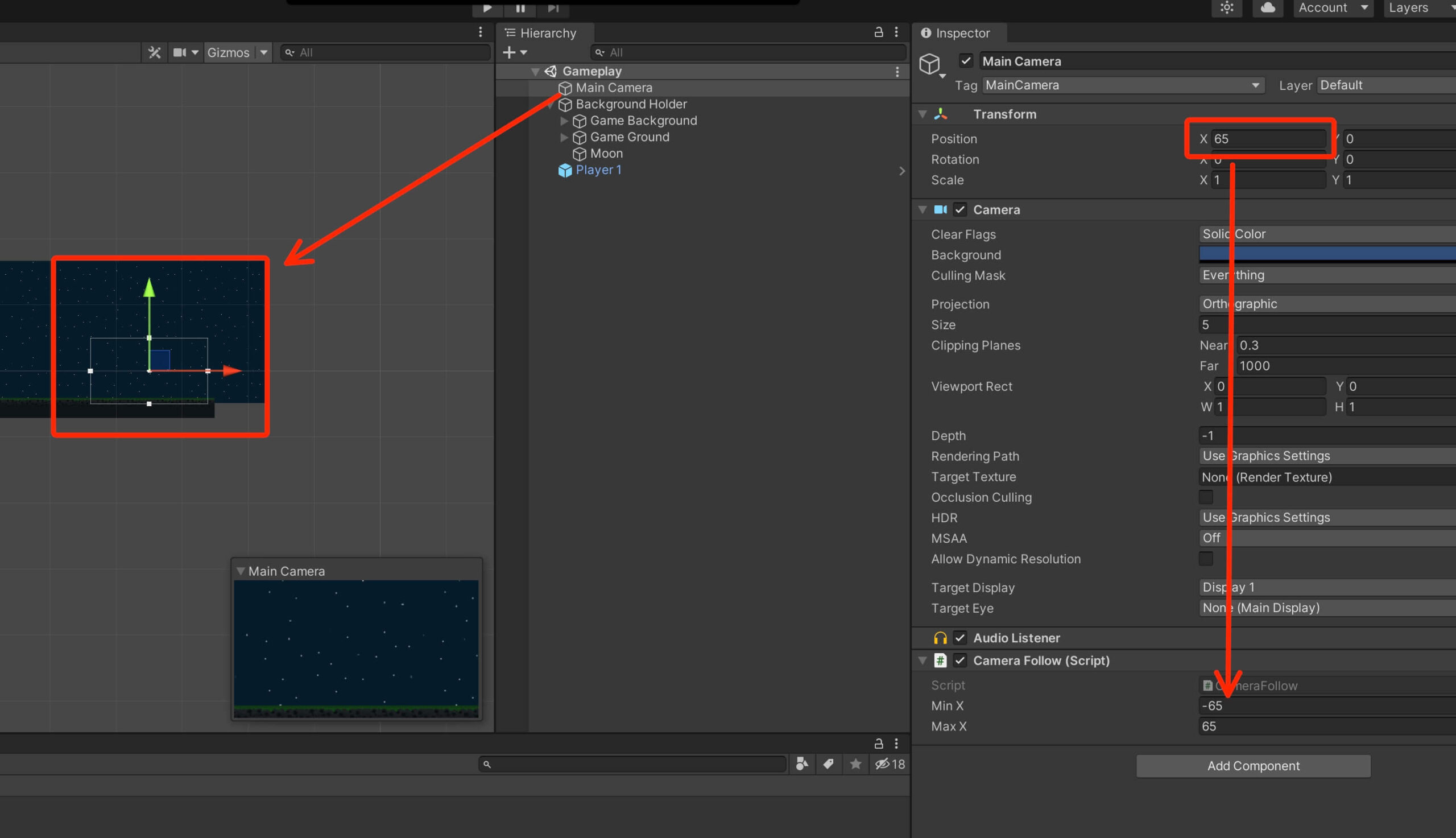
private float minX, maxX;
The playerTarget variable will represent the Player 1 or Player 2 game object’s transform property.
The tempPos variable will represent the temporary position of the camera game object.
And the minX and maxX variables will strict the camera’s movement and determine up to where the camera can move on the left and the right side.
You will notice that I didn’t set a value for the minX and maxX, but I added SerializeField above them which means we can edit their values in the Inspector tab.
To determine up to where the camera will follow the player character we can simply take the Main Camera game object, move it to the edge of the level up to where it will follow the player character and then use the X position value as the minX and the maxX when dealing with the left and the right side:
As you can see from the image above, I’ve moved the Main Camera object to the edge on the right side and took the value of the position X property, which is 65 and set that value as the maxX.
For the minX, we can use the negative of the maxX value which in this case is -65. You can test this out on your own and enter -65 in the X position of the Main Camera and you will see that it will position the camera to the edge on the left side.
You don’t have to use the exact same values as I am using, maybe you created a larger level and 65 value for the maxX and -65 value for the minX is too small for your level, so test this out on your own and set the appropriate values in the appropriate fields.
As for me, I am going to set 65 and -65 for maxX and minX:
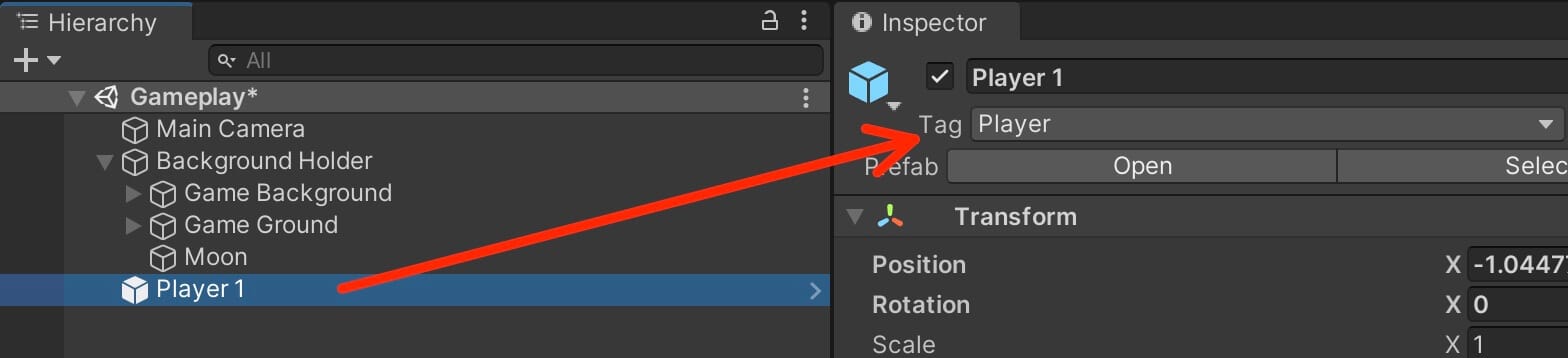
Next we need to get a reference to the player’s transform component. We are going to search for the player character via its tag, so we need to tag the player.
We already have the Player tag by default, so make sure that you select the Player 1 game object in the Hierarchy and tag him with the Player tag:
Don’t forget to override the changes for the Player 1 prefab and all the changes we make to Player 1, do the same changes to Player 2 game object as the steps are the same.
Inside the TagManager script add the following line of code:
public static string PLAYER_TAG = "Player";
Now we can get a reference to the transform component. Inside the Start function in the CameraFollow script, add the following line of code:
void Start()
{
playerTarget = GameObject.FindWithTag(TagManager.PLAYER_TAG).transform;
}
The FindWithTag function will search for a game object inside the Scene that has the specified tag that we provided as a parameter and it will return that game object, or it will return null if we don’t have a game object with the specified tag.
When we get a reference to the Player 1 game object, then we call its transform property to get a reference to it.
Now we can write code that will make the Main Camera follow the player character:
void LateUpdate()
{
if (!playerTarget)
return;
tempPos = transform.position;
tempPos.x = playerTarget.position.x;
if (tempPos.x < minX)
tempPos.x = minX;
if (tempPos.x > maxX)
tempPos.x = maxX;
transform.position = tempPos;
}
The first thing that we are doing is we are testing if we have the playerTarget. The !playerTarget is essentially testing if playerTarget != null, so using the ! in front of the object or using != null to perform a test if the object is not null are the same thing.
The reason why we are doing this is because when any of the enemies touches the player, the player will be destroyed and removed from the game.
Since the CameraFollow script depends on the player’s transform to follow the player, if we don’t perform the check at line 4 in the code above, we will get a null reference exception meaning we are trying to access the transform of the player game object while the player has been destroyed and removed from the game.
Next we get the current value of the position of the camera game object by calling transform.position and store that value in the tempPos variable.
After that we set the X property of the tempPos variable to be equal to the player’s current X position because we want to make the camera follow the player character left and right.
Then we test if the X position of tempPos is greater than the maxX and if that is true we set the X value of tempPos variable to maxX which means it will not allow it to go above the value of maxX.
We are doing the same thing for the minX but we are testing if the X value of tempPos is less than minX and if it’s true we set the X value of tempPos to minX which means it will not allow it to go below the value of minX.
And the we simply reassign the tempPos value back to the transform.position of the camera game object.
One thing that you will notice is that I am using the LateUpdate function instead of the Update function which is a better approach when you have any kind of code that is designed to follow another game object.
Update, FixedUpdate And LateUpdate
To understand why I used the LateUpdate instead of the Update function to make the camera follow the player we need to know what is the difference between the 3 available Update functions that we have in Unity.
Update Function:
The Update function is called once per frame from every script in which it is defined. The time interval to call the Update function is not fixed, it depends on how much time is required to complete the individual frame.
If a frame takes a longer or shorter time to process as compared to other frames, then the update time interval becomes different for frames. We can use Time.deltaTime to get the time in seconds it took to complete the last frame.
That is why when we moved the player character in the Update function I multiplied the moveSpeed with Time.deltaTime to make the player’s movement frame independent.
FixedUpdate Function:
The FixedUpdate function is independent from the frame rate. The time interval to call the FixedUpdate function is constant and you cat it up by going to Edit -> Project Settings -> Time:
Because we can control the time interval that is used to call FixedUpdate it is possible to call the FixedUpdate function more often the the Update function.
LateUpdate Function:
The LateUpdate function is also called once per frame but it is called after all other Update functions have been called. Which means any calculation that happens in the Update function will finish by the time the LateUpdate function gets called.
Going Back To CameraFollow Script
Taking into consideration what we learned about the Update functions above, in our case we set the player’s movement in the Update function, and the camera follow code in the LateUpdate, which means that the player’s position is already calculated by the time LateUpdate is called and this is why it is better to call any follow logic inside the LateUpdate function.
So now, let’s run the game and test the camera follow functionality:
And with that we have finished the CameraFollow script. I will leave the complete CameraFollow script below if you need to copy any line of code in your project:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CameraFollow : MonoBehaviour
{
private Transform playerTarget;
private Vector3 tempPos;
[SerializeField]
private float minX, maxX;
// Start is called before the first frame update
void Start()
{
playerTarget = GameObject.FindWithTag(TagManager.PLAYER_TAG).transform;
}
// Update is called once per frame
void LateUpdate()
{
if (!playerTarget)
return;
tempPos = transform.position;
tempPos.x = playerTarget.position.x;
if (tempPos.x < minX)
tempPos.x = minX;
if (tempPos.x > maxX)
tempPos.x = maxX;
transform.position = tempPos;
}
} // class
Where To Go From Here
In this part of the tutorial we created the player’s movement and jump functionality.
We also animated the player’s movement and we made the camera follow the player character in the game.
In the next tutorial titled Preparing And Animating The Enemies we are going to prepare and animate the enemy game objects.
